Überblick
Die Standardabweichung ist eine grundlegende statistische Kennzahl, die verwendet wird, um die Streuung oder Variation von Datenpunkten in einem Datensatz zu quantifizieren. Sie gibt an, wie stark die Werte in einem Datensatz um ihren Mittelwert streuen. Eine niedrige Standardabweichung bedeutet, dass die Datenpunkte nahe am Mittelwert liegen, während eine hohe Standardabweichung auf eine größere Streuung hinweist. Die Standardabweichung ist ein zentrales Maß in der deskriptiven Statistik und findet Anwendung in verschiedenen Bereichen wie Wirtschaft, Wissenschaft, Ingenieurwesen und Sozialwissenschaften.
Die Berechnung der Standardabweichung erfolgt in mehreren Schritten, die eine genaue Analyse der Daten ermöglichen. Durch das Verständnis und die Anwendung der Standardabweichung können wichtige Erkenntnisse über die Verteilung und Variabilität von Daten gewonnen werden, was für die Entscheidungsfindung und Risikoanalyse von entscheidender Bedeutung ist.

Konzept
Das Konzept der Standardabweichung basiert auf der Messung der Abweichungen der einzelnen Datenpunkte vom Mittelwert des Datensatzes. Diese Abweichungen werden quadriert, um negative Werte zu eliminieren, summiert und anschließend wird der Durchschnitt dieser quadrierten Abweichungen berechnet. Die Standardabweichung ist die Quadratwurzel dieser durchschnittlichen quadrierten Abweichungen und gibt somit die durchschnittliche Abweichung der Datenpunkte vom Mittelwert an.
Berechnung der Standardabweichung
Die Berechnung der Standardabweichung kann in zwei Kategorien unterteilt werden: Stichprobenstandardabweichung und Populationsstandardabweichung. Der Unterschied liegt in der Art der Daten, die analysiert werden (Stichprobe oder gesamte Population), und in der Berechnungsmethode:
- Populationsstandardabweichung: Wird verwendet, wenn die gesamte Population analysiert wird. Die Berechnung erfolgt wie folgt:
- Schritt 1: Berechnung des Mittelwerts µ der Daten:

wobei (N) die Anzahl der Datenpunkte und xi die einzelnen Datenpunkte sind.
- Schritt 2: Berechnung der Abweichungen der Datenpunkte vom Mittelwert und deren Quadrierung:

- Schritt 3: Berechnung des Durchschnitts der quadrierten Abweichungen σ2:

- Schritt 4: Ziehen der Quadratwurzel der Varianz, um die Standardabweichung σ zu erhalten:
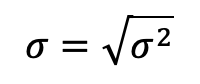
- Stichprobenstandardabweichung: Wird verwendet, wenn nur eine Stichprobe der Population analysiert wird. Die Berechnung erfolgt ähnlich, jedoch wird anstelle von (N) (Anzahl der Datenpunkte) (n-1) verwendet, um die Schätzung für die gesamte Population zu korrigieren:
- Schritt 1: Berechnung des Stichprobenmittelwerts x̄:

- Schritt 2: Berechnung der quadrierten Abweichungen vom Stichprobenmittelwert:
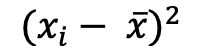
- Schritt 3: Berechnung der Varianz der Stichprobe s2:
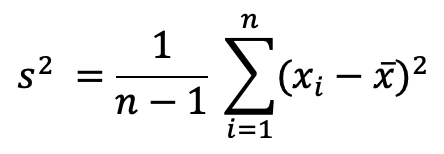
- Schritt 4: Ziehen der Quadratwurzel, um die Stichprobenstandardabweichung (s) zu erhalten:

Interpretation der Standardabweichung
Die Standardabweichung ist ein Maß für die Variabilität der Daten:
-

Vielleicht interessant für Sie Kleine Standardabweichung: Weist darauf hin, dass die Datenpunkte nahe am Mittelwert liegen, was auf eine geringe Streuung hindeutet. In vielen Anwendungen bedeutet dies eine hohe Präzision oder Konsistenz der Daten.
- Große Standardabweichung: Weist auf eine breite Streuung der Datenpunkte hin, was bedeutet, dass sie weiter vom Mittelwert entfernt liegen. Dies kann in vielen Kontexten auf eine hohe Variabilität oder Unsicherheit hinweisen.
In der Praxis wird die Standardabweichung häufig zur Bewertung von Risiken und Unsicherheiten verwendet. In der Finanzwelt dient sie beispielsweise zur Messung der Volatilität von Anlageerträgen, wobei eine höhere Standardabweichung eine höhere Risikobereitschaft impliziert. In der Qualitätskontrolle kann die Standardabweichung verwendet werden, um die Streuung von Produktionsprozessen zu überwachen und sicherzustellen, dass sie innerhalb akzeptabler Toleranzen bleibt.
In der Forschung und Wissenschaft hilft die Standardabweichung bei der Interpretation der Verteilung von Daten. Sie gibt Einblicke in die Präzision von Messungen und Experimente und ist ein Schlüsselwerkzeug in der statistischen Analyse und Hypothesentests.
Mehrwert
Die Standardabweichung bietet eine Reihe von Vorteilen für die Analyse und Interpretation von Daten:
- Messung der Variabilität: Sie bietet ein objektives Maß für die Streuung von Daten, das in vielen Bereichen der Statistik und Datenanalyse von grundlegender Bedeutung ist.
- Vergleich von Datensätzen: Die Standardabweichung ermöglicht es, die Variabilität zwischen verschiedenen Datensätzen oder Variablen zu vergleichen, selbst wenn sie unterschiedliche Mittelwerte haben.
- Risikobewertung: In der Finanzwelt und anderen Bereichen mit Unsicherheiten kann die Standardabweichung als Maß für das Risiko verwendet werden, da sie die Volatilität und die potenzielle Abweichung von erwarteten Ergebnissen quantifiziert.
- Qualitätskontrolle: In der Produktion und Fertigung hilft die Standardabweichung, Prozesse zu überwachen und sicherzustellen, dass sie konsistent und innerhalb der festgelegten Toleranzen arbeiten.
- Statistische Inferenz: In der inferentiellen Statistik wird die Standardabweichung verwendet, um Konfidenzintervalle zu berechnen und Hypothesentests durchzuführen, was entscheidend für die Ableitung von Schlussfolgerungen aus Stichprobendaten ist.

Trotz ihrer Nützlichkeit gibt es auch Herausforderungen und Einschränkungen bei der Verwendung der Standardabweichung:
- Empfindlichkeit gegenüber Ausreißern: Die Standardabweichung kann durch extreme Werte oder Ausreißer stark beeinflusst werden, was zu einer Verzerrung des Maßes führen kann.
- Voraussetzung der Normalverteilung: In vielen Anwendungen wird die Standardabweichung unter der Annahme einer Normalverteilung der Daten verwendet. Diese Annahme kann in der Praxis jedoch nicht immer zutreffen.
- Interpretation im Kontext: Die Standardabweichung allein gibt keinen Hinweis auf den Mittelwert oder die Verteilung der Daten. Ihre Interpretation erfordert daher immer den Kontext der spezifischen Datensätze und deren Charakteristika.
Die Standardabweichung ist ein grundlegendes und vielseitiges statistisches Maß, das in vielen Bereichen der Wissenschaft und Praxis verwendet wird. Sie bietet wertvolle Einblicke in die Streuung und Variabilität von Daten und ist ein unverzichtbares Werkzeug für die Analyse und Interpretation von Datensätzen. Trotz einiger Herausforderungen und Einschränkungen bleibt die Standardabweichung ein zentrales Element der Statistik und spielt eine Schlüsselrolle bei der Entscheidungsfindung und Risikoanalyse. Die Standardabweichung spielt gerade zur Bewertung von Prozessen im Six Sigma eine entscheidende Rolle.